Linear neuron weights learning
Table of Contents
- Learning the weights of a linear neuron
- Why the perceptron learning procedure cannot be generalised to hidden layers
- A different way to show that a learning procedure makes progress
- Linear neurons (also called linear filters)
- Why don’t we solve it analytically?
- A toy example to illustrate the iterative method
- Solving the equations iteratively
- The true weights used by the cashier
- A model of the cashier with arbitrary initial weights
- The error surface for a linear neuron
- Learning the weights of a logistic output neuron
- The backpropagation algorithm
- How to use the derivatives computed by the backpropagation algorithm
Learning the weights of a linear neuron
Why the perceptron learning procedure cannot be generalised to hidden layers
• The perceptron convergence procedure works by ensuring that every time the weights change, they get closer to every “generously feasible” set of weights.
– This type of guarantee cannot be extended to more complex networks in which the average of two good solutions may be a bad solution.
• So “multi-layer” neural networks do not use the perceptron learning procedure.
– They should never have been called multi-layer perceptrons.
A different way to show that a learning procedure makes progress
• Instead of showing the weights get closer to a good set of weights, show that the actual output values get closer the target values.
– This can be true even for non-convex problems in which there are many quite different sets of weights that work well and averaging two good sets of weights may give a bad set of weights. – It is not true for perceptron learning.
• The simplest example is a linear neuron with a squared error measure.
Linear neurons (also called linear filters)
• The neuron has a real- valued output which is a weighted sum of its inputs
• The aim of learning is to minimize the error summed over all training cases.
– The error is the squared difference between the desired output and the actual output. weight vector y = ∑ wixi = wTx
Why don’t we solve it analytically?
• It is straight-forward to write down a set of equations, one per training case, and to solve for the best set of weights.
– This is the standard engineering approach so why don’t we use it?
• Scientific answer: We want a method that real neurons could use. • Engineering answer: We want a method that can be generalized to multi-layer, non-linear neural networks.
- The analytic solution relies on it being linear and having a squared error measure.
- Iterative methods are usually less efficient but they are much easier to generalize.
A toy example to illustrate the iterative method
• Each day you get lunch at the cafeteria.
– Your diet consists of fish, chips, and ketchup. You get several – portions of each.
• The cashier only tells you the total price of the meal
– After several days, you should be able to figure out the price of each portion.
• The iterative approach: Start with random guesses for the prices and then adjust them to get a better fit to the observed prices of whole meals.
Solving the equations iteratively
• Each meal price gives a linear constraint on the prices of the portions:
price = xfishwfish + xchipswchips + xketchupwketchup
• The prices of the portions are like the weights in of a linear neuron.
w = (wfish , wchips , wketchup)
• We will start with guesses for the weights and then adjust the guesses slightly to give a better fit to the prices given by the cashier.
The true weights used by the cashier
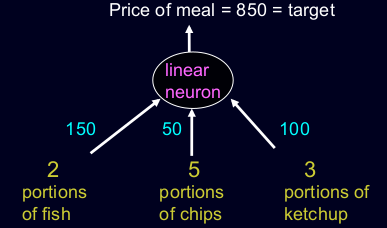
Figure 1: Graphical representation
A model of the cashier with arbitrary initial weights
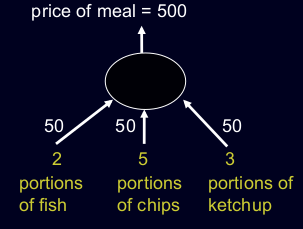
Figure 2: First iteration
• Residual error = 350 • The “delta-rule” for learning is: price of meal = 500 Δw i = ε x i (t − y) 50 2 portions of fish 50 5 portions of chips 50 3 portions of ketchup • With a learning rate ε of 1/35, the weight changes are +20, +50, +30 • This gives new weights of 70, 100, 80. – Notice that the weight for chips got worse!Deriving the delta rule • Define the error as the squared residuals summed over all training cases: • Now differentiate to get error derivatives for weights • The batch delta rule changes the weights in proportion to their error derivatives summed over all training cases E = 1 2 ∑ (t n − y n ) 2 n∈training ∂E 1 ∂y n dE n = 2 ∑ n ∂w i ∂w dy i n = − ∑ x in (t n − y n ) n Δw i = − ε ∂E = ∑ ε x in (t n − y n ) ∂w i nBehaviour of the iterative learning procedure • Does the learning procedure eventually get the right answer? – There may be no perfect answer. – By making the learning rate small enough we can get as close as we desire to the best answer. • How quickly do the weights converge to their correct values? – It can be very slow if two input dimensions are highly correlated. If you almost always have the same number of portions of ketchup and chips, it is hard to decide how to divide the price between ketchup and chips.The relationship between the online delta-rule and the learning rule for perceptrons • In perceptron learning, we increment or decrement the weight vector by the input vector. – But we only change the weights when we make an error. • In the online version of the delta-rule we increment or decrement the weight vector by the input vector scaled by the residual error and the learning rate. – So we have to choose a learning rate. This is annoying.Neural Networks for Machine Learning Lecture 3b
The error surface for a linear neuron
Geoffrey Hinton with Nitish Srivastava Kevin SwerskyThe error surface in extended weight space • The error surface lies in a space with a horizontal axis for each weight and one vertical axis for the error. – For a linear neuron with a squared error, it is a quadratic bowl. – Vertical cross-sections are parabolas. – Horizontal cross-sections are ellipses. • For multi-layer, non-linear nets the error surface is much more complicated. E w1 w2Online versus batch learning • The simplest kind of batch learning does steepest descent on the error surface. • The simplest kind of online learning zig-zags around the direction of steepest descent: – This travels perpendicular to constraint from the contour lines. training case 1 w1 w1 w2 constraint from training case 2 w2Why learning can be slow • If the ellipse is very elongated, the direction of steepest descent is almost perpendicular to the direction towards the minimum! – The red gradient vector has a large component along the short axis of the ellipse and a small component along the long axis of the ellipse. – This is just the opposite of what we want. w1 w2Neural Networks for Machine Learning Lecture 3c
Learning the weights of a logistic output neuron
Geoffrey Hinton with Nitish Srivastava Kevin SwerskyLogistic neurons • These give a real-valued output that is a smooth and bounded function of their total input. – They have nice derivatives which make learning easy. y = z = b + ∑ x i w i 1 + e i 1 y 0.5 0 1 0 z −zThe derivatives of a logistic neuron • The derivatives of the logit, z, with respect to the inputs and the weights are very simple: z = b + ∑ x i w i i ∂z = x i ∂w i • The derivative of the output with respect to the logit is simple if you express it in terms of the output: 1 y = 1 + e ∂z = w i ∂x i −z dy = y ( 1 − y) dzThe derivatives of a logistic neuron y = 1 1 + e −z = ( 1 + e −z ) −1 " 1 % " e −z % dy − 1 (−e −z ) ' = y(1− y) = = $ ' $$ ' −z 2 −z −z dz
& ( 1 + e ) 1 + e
e −z (1+ e −z ) −1 (1+ e −z ) −1 = = = 1− y because −z −z −z 1 + e −z 1 + e 1 + e 1 + eUsing the chain rule to get the derivatives needed for learning the weights of a logistic unit • To learn the weights we need the derivative of the output with respect to each weight: ∂y ∂z dy = = x i y (1− y) ∂w i ∂w i dz delta-rule ∂E = ∂w i ∑ n ∂y n ∂E n n n n n = − x y (1− y ) (t − y ) ∑ i n ∂w i ∂y n extra term = slope of logisticNeural Networks for Machine Learning Lecture 3d
The backpropagation algorithm
Geoffrey Hinton with Nitish Srivastava Kevin SwerskyLearning with hidden units (again) • Networks without hidden units are very limited in the input-output mappings they can model. • Adding a layer of hand-coded features (as in a perceptron) makes them much more powerful but the hard bit is designing the features. – We would like to find good features without requiring insights into the task or repeated trial and error where we guess some features and see how well they work. • We need to automate the loop of designing features for a particular task and seeing how well they work.Learning by perturbing weights (this idea occurs to everyone who knows about evolution) • Randomly perturb one weight and see if it improves performance. If so, save the change. – This is a form of reinforcement learning. – Very inefficient. We need to do multiple forward passes on a representative set of training cases just to change one weight. Backpropagation is much better. – Towards the end of learning, large weight perturbations will nearly always make things worse, because the weights need to have the right relative values. output units hidden units input unitsLearning by using perturbations • We could randomly perturb all the weights in parallel and correlate the performance gain with the weight changes. – Not any better because we need lots of trials on each training case to “see” the effect of changing one weight through the noise created by all the changes to other weights. • A better idea: Randomly perturb the activities of the hidden units. – Once we know how we want a hidden activity to change on a given training case, we can compute how to change the weights. – There are fewer activities than weights, but backpropagation still wins by a factor of the number of neurons.The idea behind backpropagation • We don’t know what the hidden units ought to do, but we can compute how fast the error changes as we change a hidden activity. – Instead of using desired activities to train the hidden units, use error derivatives w.r.t. hidden activities. – Each hidden activity can affect many output units and can therefore have many separate effects on the error. These effects must be combined. • We can compute error derivatives for all the hidden units efficiently at the same time. – Once we have the error derivatives for the hidden activities, its easy to get the error derivatives for the weights going into a hidden unit.Sketch of the backpropagation algorithm on a single case • First convert the discrepancy between each output and its target value into an error derivative. • Then compute error derivatives in each hidden layer from error derivatives in the layer above. • Then use error derivatives w.r.t. activities to get error derivatives w.r.t. the incoming weights. E = 1 2 (t j − y j ) 2 ∑ j∈output ∂E = −(t j − y j ) ∂y j ∂E ∂y j ∂E ∂y iBackpropagating dE/dy y j j z j y i i dy j ∂E ∂E ∂E = = y j (1− y j ) ∂z j dz j ∂y j ∂y j ∂E = ∂y i dz j ∂E ∑ dy ∂z = i j j ∑ w ij j ∂z j ∂E ∂E ∂E = = y i ∂w ij ∂w ij ∂z j ∂z j ∂E ∂z jNeural Networks for Machine Learning Lecture 3e
How to use the derivatives computed by the backpropagation algorithm
Geoffrey Hinton with Nitish Srivastava Kevin SwerskyConverting error derivatives into a learning procedure • The backpropagation algorithm is an efficient way of computing the error derivative dE/dw for every weight on a single training case. • To get a fully specified learning procedure, we still need to make a lot of other decisions about how to use these error derivatives: – Optimization issues: How do we use the error derivatives on individual cases to discover a good set of weights? (lecture 6) – Generalization issues: How do we ensure that the learned weights work well for cases we did not see during training? (lecture 7) • We now have a very brief overview of these two sets of issues.Optimization issues in using the weight derivatives • How often to update the weights – Online: after each training case. – Full batch: after a full sweep through the training data. – Mini-batch: after a small sample of training cases. • How much to update (discussed further in lecture 6) – Use a fixed learning rate? – Adapt the global learning rate? – Adapt the learning rate on each connection separately? – Don’t use steepest descent? w1 w2Overfitting: The downside of using powerful models • The training data contains information about the regularities in the mapping from input to output. But it also contains two types of noise. – The target values may be unreliable (usually only a minor worry). – There is sampling error. There will be accidental regularities just because of the particular training cases that were chosen. • When we fit the model, it cannot tell which regularities are real and which are caused by sampling error. – So it fits both kinds of regularity. – If the model is very flexible it can model the sampling error really well. This is a disaster .A simple example of overfitting input = x Which output value should you predict for this test input? • Which model do you trust? – The complicated model fits the data better. – But it is not economical. • A model is convincing when it fits a lot of data surprisingly well. – It is not surprising that a complicated model can fit a small amount of data well.Ways to reduce overfitting • A large number of different methods have been developed. – Weight-decay – Weight-sharing – Early stopping – Model averaging – Bayesian fitting of neural nets – Dropout – Generative pre-training • Many of these methods will be described in lecture 7.
blog comments powered by Disqus