Recurrent neural networks brief overview
Table of Contents
- Modeling sequences: A brief overview
- Getting targets when modeling sequences
- Memoryless models for sequences
- Beyond memoryless models
- Linear Dynamical Systems(engineers love them!)
- Hidden Markov Models (computer scientists love them!)
- A fundamental limitation of HMMs
- Recurrent neural networks
- Do generative models need to be stochastic?
- Recurrent neural networks
- Transcript
- Training RNNs with backpropagation
- A toy example of training an RNN
- Why it is difficult to train an RNN
Modeling sequences: A brief overview
Getting targets when modeling sequences
When applying machine learning to sequences, we often want to turn an input sequence into an output sequence that lives in a different domain.
- E. g. turn a sequence of sound pressures into a sequence of word identities. When there is no separate target sequence, we can get a teaching signal by trying to predict the next term in the input sequence.
- The target output sequence is the input sequence with an advance of 1 step.
- This seems much more natural than trying to predict one pixel in an image from the other pixels, or one patch of an image from the rest of the image.
- For temporal sequences there is a natural order for the predictions. Predicting the next term in a sequence blurs the distinction between supervised and unsupervised learning.
- It uses methods designed for supervised learning, but it doesn’t require a separate teaching signal.
Memoryless models for sequences
Autoregressive models w t −1 w t −2 Predict the next term in a sequence from a fixed number of input(t-2) input(t-1) previous terms using “delay taps”.
Feed-forward neural nets These generalize autoregressive models by using one or more layers of non-linear hidden units. e.g. Bengio’s first language model. input(t) hidden input(t-2) input(t-1) input(t)
Beyond memoryless models
• If we give our generative model some hidden state, and if we give this hidden state its own internal dynamics, we get a much more interesting kind of model.
- It can store information in its hidden state for a long time.
- If the dynamics is noisy and the way it generates outputs from its hidden state is noisy, we can never know its exact hidden state.
- The best we can do is to infer a probability distribution over the space of hidden state vectors.
This inference is only tractable for two types of hidden state model.
- The next three slides are mainly intended for people who already know about these two types of hidden state model. They show how RNNs differ.
- Do not worry if you cannot follow the details.
Linear Dynamical Systems(engineers love them!)
time →
• These are generative models. They have a real-valued hidden state that cannot be observed directly.
- The hidden state has linear dynamics with Gaussian noise and produces the observations using a linear model with Gaussian noise.
- There may also be driving inputs.
• To predict the next output (so that we can shoot down the missile) we need to infer the hidden state.
- A linearly transformed Gaussian is a Gaussian. So the distribution over the hidden
Hidden Markov Models (computer scientists love them!)
time →
• Hidden Markov Models have a discrete one-of-N hidden state. Transitions between states are stochastic and controlled by a transition matrix. The outputs produced by a state are stochastic.
- We cannot be sure which state produced a given output. So the state is “hidden”.
- It is easy to represent a probability distribution across N states with N numbers.
• To predict the next output we need to infer the probability distribution over hidden states.
- HMMs have efficient algorithms for
A fundamental limitation of HMMs
Consider what happens when a hidden Markov model generates data.
- At each time step it must select one of its hidden states. So with N hidden states it can only remember log(N) bits about what it generated so far.
• Consider the information that the first half of an utterance contains about the second half:
- The syntax needs to fit (e.g. number and tense agreement).
- The semantics needs to fit. The intonation needs to fit.
- The accent, rate, volume, and vocal tract characteristics must all fit.
• All these aspects combined could be 100 bits of information that the first half of an utterance needs to convey to the second half. 2100
Recurrent neural networks
time →
• RNNs are very powerful, because they combine two properties:
- Distributed hidden state that allows them to store a lot of information about the past efficiently.
- Non-linear dynamics that allows them to update their hidden state in complicated ways.
• With enough neurons and time, RNNs can compute anything that can be computed by your computer.
Do generative models need to be stochastic?
• Linear dynamical systems and hidden Markov models are stochastic models.
- But the posterior probability distribution over their hidden states given the observed data so far is a deterministic function of the data.
Recurrent neural networks are deterministic.
- So think of the hidden state of an RNN as the equivalent of the deterministic probability distribution over hidden states in a linear dynamical system or hidden Markov model.
Recurrent neural networks
What kinds of behaviour can RNNs exhibit?
- They can oscillate. Good for motor control?
- They can settle to point attractors. Good for retrieving memories?
- They can behave chaotically. Bad for information processing?
- RNNs could potentially learn to implement lots of small programs that each capture a nugget of knowledge and run in parallel, interacting to produce very complicated effects.
But the computational power of RNNs makes them very hard to train.
- For many years we could not exploit the computational power of RNNs despite some heroic efforts (e.g. Tony Robinson’s speech recognizer).
Transcript
In this video, I am going to give an overview of various types of models that have been used for sequences. I'll start with the simplest kinds of model, which is ultra aggressive models, that just try and predict the next term or the sequence from previous terms. I'll talk about more elaborate variants of them using hidden units.
And then I'll talk about, more interesting kinds of models, that have hidden state, and hidden dynamics. These include linear dynamical systems and hidden Markov models. Most of these are quite complicated kinds of models, and I don't expect you to understand all the details of them. The main point of mentioning them is to be able to show how recurrent your own networks are related to models of that kind.
When we're using machine learning to model sequences, we often want to turn one sequence into another sequence. For example, we might want to turn English words into French words or we might want to take a sequence of sound pressures and turn it into a sequence of word identities which is what's happening in speech recognition.
Sometimes we don't have a separate target sequence, and in that case we can get a teaching signal by trying to predict the next term in the input sequence. So the target output sequence is simply the input sequence with an advance of one time step. This seems much more natural, than trying to predict one pixel in an image from all the other pixels or one patch of an image from the rest of the image. One reason it probably seems more natural is that for temporal sequences, there is a natural order to do the predictions in.
Whereas for images it's not clear what you should predict from what. But in fact a similar approach works very well for images. When we predict the next term in a sequence, it blurs the distinction, between supervised and unsupervised learning, that I made at beginning of the course. So we use methods that were designed for supervised learning to predict the next term. But we don't require separate teaching signal. So in that sense, it's unsupervised.
I'm now going to give a quick review of some of the, other models of sequences, before we get on to using recurrent neural nets to model sequences. So a nice simple model for sequences that doesn't have any memory is an auto regressive model. What that does is take some previous terms in the sequence and try and predict the next term basically as a weighted average of previous terms. The previous terms might be individual values or they might be whole vectors.
And a linear auto regressive model would just take a weighted average of those to predict the next term. We can make that considerably more complicated by adding hidden units. So in a feedforward neural net, we might take some previous input terms, put them through some hidden units, and predict the next term. Memory list models are only one subclass of models that can be used for sequences. We can think about ways of generating sequences, and one very natural way to generate a sequence is to have a model that has some hidden state which has its own internal dynamics. So, the hidden state evolves according to its internal dynamics, and the hidden state also produces observations, and we get to see those observations.
That's a much more interesting kind of model. It can store information in its hidden state for a long time. Unlike the memoryless models, there's no simple band, to how far we have to look back before we can be sure it's not affecting things. If the dynamics of the hidden state is noisy and the way it generates outputs from its hidden state is noisy, then by observing the output of a generative model like this, you can never know for sure what it's hidden state was.
The best you can do is to infer probability distribution over the space of all possible hidden state vectors. You can know that it's probably in some part of the space and not another part of the space, but you can't pin it down exactly. So with a generative model like this, if you get to observe what it produces, and you now try to infer what the hidden state was, in general that's very hard, but there's two types of hidden state model for which the computation is tractable.
That is, there's a fairly straightforward computation that allows you to infer the probability distribution over the hidden state vectors that might have caused the data. Of course when we do this and apply it to real data. We're assuming that the real data is generated by our model. So that's typically what we do when we're modeling things. /We assume the data was generated by the model and then we infer what state the model must have been in, in order to generate that data./
The next three slides are mainly intended for people who already know about the two types of hidden state model I'm going to describe. The point of the slides is so that I make it clear how recurrent neural networks differ from those standard models. If you can't follow the details of the two standard models, don't worry too much. That's not the main point.
So one standard model is a linear dynamical system. It's very widely used in engineering. This is a generative model that has real valued hidden state. The hidden state has linear dynamics, shown by those red arrows on the right. And the dynamics has Gaussian noise, so that the hidden state evolves probabilistically.
There may also be driving inputs, shown at the bottom there, which directly influence the hidden state. So the inputs, influence the hidden state directly, the hidden state determines the output to predict the next output of a system like this, we need to be able to infer its hidden state. And these kinds of systems are used, for example, for tracking missiles.
In fact, one of the earliest uses of Gaussian distributions was for trying to track planets from noisy observations. Gaussian actually figured out that, if you assume Gaussian noise, you could do a good job of that. One nice property that a Gaussian has is that if you linearly transform a Gaussian you get another Gaussian. Because all the noise in a linear dynamic system is Gaussian. It turns out that the distribution over the hidden state given the observation so far, that is given the output so far, is also a Gaussian. It's a full covariance Gaussian, and it's quite complicated to compute what it is.
But it can be computed efficiently. And there's a technique called Kalman Filtering. This is an efficient recursive way of updating your representation of the hidden state given a new observation. So, to summarize, Given observations of the output of the system, we can't be sure what hidden state it was in, but we can, estimate a Gaussian distribution over the possible hidden states it might have been in.
Always assuming, of course, that our model is a correct model of the reality we're observing. A different kind of hidden state model that uses discrete distributions rather than Gaussian distributions, is a hidden Markov model. And because it's based on discrete mathematics, computer scientists love these ones. In a hidden Markov model, the hidden state consists of a one of N choice. So there a number of things called states. And the system is always in exactly one of those states. The transitions between states are probabilistic. They're controlled by a transition matrix which is simply a bunch of probabilities that say, if you're in state one at time one, What's the probability of you going to state three at time two? The output model is also stochastic.
So, the state that the system is in doesn't completely determine what output it produces. There's some variation in the output that each state can produce. Because of that, we can't be sure which state produced a given output. In a sense, the states are hidden behind this probabilistic veil, and that's why they're called hidden. Historically the reason hidden units in a neural network are called hidden, is because I like this term. It sounded mysterious, so I stole it from neural networks.
It is easy to represent the probability distribution across n states with n numbers. So, the nice thing about a hidden Markov model, is we can represent the probability distribution across its discreet states. So, even though we don't know what it, what state it's in for sure, we can easily represent the probability distribution. And to predict the next output from a hidden Markov model, we need to infer what hidden state it's probably in. And so we need to get our hands on that probability distribution. It turns out there's an easy method based on dynamic programming that allows us to take the observations we've made and from those compute the probability distribution across the hidden states.
Once we have that distribution, there is a nice elegant learning algorithm hidden Markov models, and that's what made them so appropriate for speech. And in the 1970s, they took over speech recognition. There's a fundamental limitation of HMMs. It's easiest to understand this limitation, if we consider what happens when a hidden Markov model generates data. At each time step when it's generating, it selects one of its hidden states. So if it's got N hidden states, the temporal information stored in the hidden state is at most log(N) n bits.
So that's all it knows about what it's done so far. So now let's consider how much information a hidden Markov model can convey to the second half of an utterance it produces from the first half. So imagine it's already produced the first half of an utterance. And now it's going to have to produce the second half. And remember, its memory of what it said for the first half is in which of the n states it's in. So its memory only has log(N) bits of information in it. To produce the second half that's compatible with the first half, we must make the syntax fit.
So for example, the number intend must agree. It also needs to make the semantics fit. It can't have the second half of the sentence be about something totally different from the first half. Also the intonation needs to fit so it would look very silly if the, intonation contour completely changed halfway through the sentence. There's a lot of other things that also have to fit. The accent of the speaker, The rate they're speaking at, How loudly they're speaking. And the vocal tract characteristics of the speaker.
All of those things must fit between the second half of the sentence and the first half. And so if you wanted a hidden Markov model to actually generate a sentence, the hidden state has to be able to convey all that information from the first half to the second half. Now the problem is that all of those aspects could easily come to a hundred bits of information. So the first half of the sentence needs to convey a hundred bits of information to the second half and that means that the hidden Markov model needs two to the hundreds states and that's just too many.
So that brings us to recurrence your own networks. They have a much more efficient way of remembering information. They're very powerful because they combine two properties that have distributed hidden state. That means, several different units can be active at once. So they can remember several different things at once. They don't just have one active unit. They're also nonlinear. You see, a linear dynamical system has a whole hidden state vector. So it's got more than one value at a time, but those values are constrained to act in a linear way so as to make inference easy, and in a recurrent neural network we allow the dynamics to be much more complicated.
With enough neurons and enough time, a recurring neuron network can compute anything that can be computed by your computer. It's a very powerful device. So linear dynamical systems and hidden Markov models are both stochastic models. That is the dynamics and the production of observations from the underlying state both involve intrinsic noise.
And the question is do models need to be like that. Well one thing to notice is that the posterior probability distribution over hidden states in either a limited anomical system or hidden Markov model is a deterministic function of the data that you've seen so far. That is the inference algorithm for these systems ends up with a probability distribution, and that probability distribution is just a bunch of numbers, and those numbers are a deterministic version of the data so far.
In a recurrent neural network, you get a bunch of numbers that are a deterministic function of the data so far. And it might be a good idea to think of those numbers that constitute the hidden state of a recurrent neural network. They're very like the probability distribution for these simple stochastic models.
So what kinds of behavior can recurrent networks exhibit? Well, they can oscillate. That's obviously good for things like motion control, where when you're walking, for example, you want to know regular oscillation, which is your stride. They can settle to point attractors. That might be good for retrieving memories. And later on in the course we'll look at Hopfield nets where they use the settling to point attractors to store memories.
So the idea is you have a sort of rough idea of what you're trying to retrieve. You then let the system settle down to a stable point and those stable points correspond to the things you know about. And so by settling to that stable point you retrieve a memory. They can also behave chaotically if you set the weights in the appropriate regime. Often, chaotic behavior is bad for information processing, because in information processing, you want to be able to behave reliably if you want to achieve something.
There are some circumstances where it's a good idea. If you're up against a much smarter adversary, you probably can't outwit them, so it might be a good idea just to behave randomly. And one way to get the appearance of randomness is to behave chaotically. One nice thing about RNN's, which, a long time ago, I thought was gonna make them very powerful, is that an RNN could learn to implement lots of little programs, using different subsets of its hidden state. And each of these little programs could capture a nugget of knowledge. And all of these things could run in parallel, and interact with each other in complicated ways.
Unfortunately the computational power of recurrent neural networks makes them very hard to train. For many years, we couldn't exploit the computational power of recurrent neural networks. It was some heroic efforts. For example, Tony Robinson managed to make quite a good speech recognizer using recurrent nets. He had to do a lot of work implementing them on a parallel computer built out of transputers. And it was only recently that people managed to produce recurrent neural networks that outperformed Tony Robinson's
Training RNNs with backpropagation
The equvalence between feedforward nets and recurrent nets
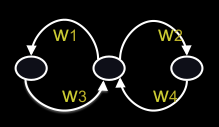
Figure 1: Recurrent Neural Network
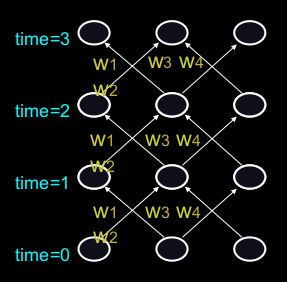
Figure 2: Recurrent Neural Network in Unwrapped Representation
Assume that there is a time delay of 1 in using each connection. The recurrent net is just a layered net that keeps reusing the same weights.
Reminder: Backpropagation with weight constraints
It is easy to modify the backprop algorithm to incorporate linear constraints between the weights.
We compute the gradients as usual, and then modify the gradients so that they satisfy the constraints.
- So if the weights started off satisfying the constraints, they will continue to satisfy them.
To constrain : w1 = w2 we need : Δw1 = Δw2 compute :
\(\frac{\partial{}E}{\partial{}w_{1}} and \frac{\partial{}E}{\partial{}w_{2}}\) use \(\frac{\partial{}E}{\partial{}w_{1}} + \frac{\partial{}E}{\partial{}w_{2}}\) for w1 and w2
Backpropagation through time
We can think of the recurrent net as a layered, feed-forward net with shared weights and then train the feed-forward net with weight constraints. We can also think of this training algorithm in the time domain:
- The forward pass builds up a stack of the activities of all the units at each time step.
- The backward pass peels activities off the stack to compute the error derivatives at each time step.
- After the backward pass we add together the derivatives at all the different times for each weight.
An irritating extra issue
We need to specify the initial activity state of all the hidden and output units. We could just fix these initial states to have some default value like 0.5. But it is better to treat the initial states as learned parameters. We learn them in the same way as we learn the weights.
- Start off with an initial random guess for the initial states.
- At the end of each training sequence, backpropagate through time
all the way to the initial states to get the gradient of the error function with respect to each initial state.
- Adjust the initial states by following the negative gradient.
Providing input to recurrent networks
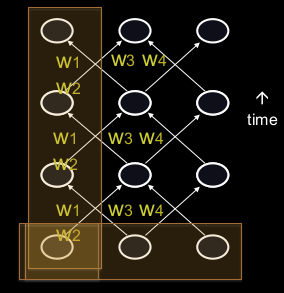
Figure 3: RNN input
We can specify inputs in several ways:
- Specify the initial states of all the units.
- Specify the initial states of a subset of the units.
- Specify the states of the same subset of the units at every time step.
This is the natural way to model most sequential data.
Teaching signals for recurrent networks
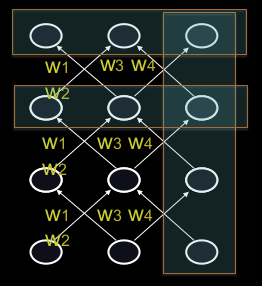
Figure 4: Teaching signals
We can specify targets in several ways:
- Specify desired final activities of all the units
- Specify desired activities of all units for the last few steps
- Good for learning attractors
- It is easy to add in extra error derivatives as we backpropagate.
- Specify the desired activity of a subset of the units.
- The other units are input or hidden units.
Transcript
In this video, I'm going to talk about the back propagation through time algorithm. It's the standard way to train or recurrence your own network.
The algorithm is really quite simple once you have seen the equivalents between a recurrent neural network and a feed forward neural network that has one layer for each time step. I'll also talk about ways of providing input, and desired outputs, to recurrent neural networks. So the diagram shows a simple recurrent net with three interconnected neurons. We're going to assume there's a time delay of one in using each of those connections and that the network runs in discrete time, so the clock that has integer ticks. The key to understanding how to train a recurrent network is to see that a recurrent network is really just the same as a feed forward network, where you've expanded the recurrent network in time. So the recurrent network starts off in some initial state. Shown at the bottom there, times zero. And then uses the way some of these connections to get a new state, shown at time one. You then uses the same weights again to get another new state, and it uses the same weights again to get another new state and so on. So it's really just a lead feed forward network, where the weight is a constraint to be the same at every layer. Now backprop is good at learning when there are weight constraints. We saw this for convolutional nets and just to remind you, we can actually incorporate any linear constraint quite easily in backprop. So we compute the gradients as usual, as if the weights were not constrained. And then we modify the gradients, so that we maintain the constraints. So if we want W1 to equal W2, we start off with an equal and then we need to make sure that the changing W1 is equal to the changing W2. And we do that by simply taking the derivative of the area with respect to W1, the derivative with respect to W2, and adding or averaging them, and then applying the same quantity for updating both W1 and W2. So if the weights started off satisfying the constraints they'll continue to satisfy the constraints. The backpropagation through time algorithm is just the name for what happens when you think of a recurrent net as a lead feet forward net with shared weights, and you train it with backpropagation. So, we can think of that algorithm in the time domain. The forward pass builds up a stack of activities at each time slice. And the backward pass peels activities off that stack and computes error derivatives each time step backwards. That's why it's called back propagation through time. After the backward pass we can add together the derivatives at all the different time step for each particular weight. And then change all the copies of that weight by the same amount which is proportional to the sum or average of all those derivatives. There is an irritating extra issue. If we don't specify the initial state of the all the units, for example, if some of them are hidden or output units, then we have to start them off in some particular state. We could just fix those initial states to have some default value like 0.5, but that might make the system work not quite as well as it would otherwise work if it had some more sensible initial value. So we can actually learn the initial states. We treat them like parameters rather than activities and we learn them the same way as learned the weights. We start off with an initial random guess for the initial states. That is the initial states of all the units that aren't input units And then at the end of each training sequence we back propagate through time all the way back to the initial states. And that gives us the gradient of the error function with respects to the initial state. We then just, adjust the initial states by following, that gradient. We go downhill in the gradient, and that gives us new initial states that are slightly different. There's many ways in which we can provide the input to a recurrent neural net. We could, for example, specify the initial state of all the units. That's the most natural thing to do when we think of a recurrent net, like a feed forward net with constrained weights. We could specify the initial state of just a subset of the units or we can specify the states at every time stamp of the subset of the units and that's probably the most natural way to input sequential data. Similarly, there's many way we can specify targets for a recurrent network. When we think of it as feed forward network with constrained weights, the natural thing to do is to specify the desired final states for all of the units. If we're trying to train it to settle to some attractor, we might want to specify the desired states not just for the final time steps but for several time steps. That will cause it to actually settle down there, rather than passing through some state and going off somewhere else. So by specifying several states of the end, we can force it to learn attractors and it's quite easy as we back propagate to add in derivatives that we get from each time stamp. So the back propegation starts at the top, with the derivatives for the final time stamp. And then as we go back through the line before the top we add in the derivatives for that man, and so on. So it's really very little extra effort to have derivatives at many different layers. Or we could specify the design activity of a subset of units which we might think of as output units. And that's a very natural way to train a recurrent neural network that is meant to be providing a continuous output.
A toy example of training an RNN
A good toy problem for a recurrent network
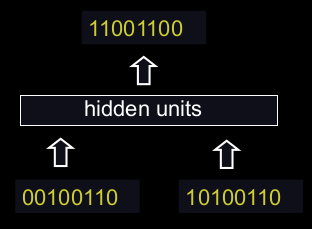
Figure 5: Binary addition
We can train a feedforward net to do binary addition, but there are obvious regularities that it cannot capture efficiently.
- We must decide in advance the maximum number of digits in each number.
- The processing applied to the beginning of a long number does not generalize to the end of the long number because it uses different weights.
As a result, feedforward nets do not generalize well on the binary addition task.
The algorithm for binary addition
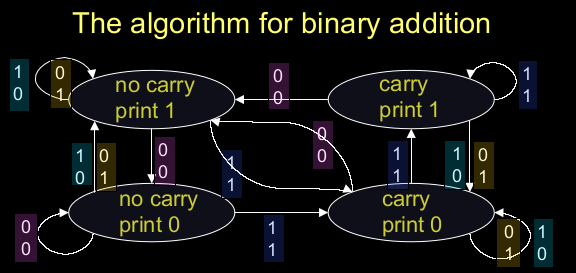
Figure 6: Binary addition algorithm
This is a finite state automaton. It decides what transition to make by looking at the next column. It prints after making the transition. It moves from right to left over the two input numbers.
A recurrent net for binary addition

Figure 7: Addition in column
The network has two input units and one output unit.
It is given two input digits at each time step.
The desired output at each time step is the output for the column that was provided as input two time steps ago.
- It takes one time step to update the hidden units based on the two input digits.
- It takes another time step for the hidden units to cause the output.
The connectivity of the network
The 3 hidden units are fully interconnected in both directions.
- This allows a hidden activity pattern at one time step to vote for the hidden activity pattern at the next time step.
The input units have feedforward connections that allow then to vote for the next hidden activity pattern. 3 fully interconnected hidden units
What the network learns
It learns four distinct patterns of activity for the 3 hidden units. These patterns correspond to the nodes in the finite state automaton.
- Do not confuse units in a neural network with nodes in a finite state automaton. Nodes are like activity vectors.
- The automaton is restricted to be in exactly one state at each time. The hidden units are restricted to have exactly one vector of activity at each time.
A recurrent network can emulate a finite state automaton, but it is exponentially more powerful. With N hidden neurons it has 2N possible binary activity vectors (but only N2 weights)
- This is important when the input stream has two separate things going on at once.
- A finite state automaton needs to square its number of states.
- An RNN needs to double its number of units.
Transcript
In this video, I'm going to describe how a recurrent neural network solves a toy problem. It's a problem that's chosen to demonstrate what it is you can do with recurrent neural networks that you cannot do conveniently with feed-forward neural networks. The problem is adding up two binary numbers. Off to the recurrent neural network, has learned to solve the problem. It's interesting to look at its hidden states, and see how they relate to the hidden states in a finite state automaton that's solving the same problem.
So consider the problem of adding up two binary numbers. We could train a feed-forward neural network to do that. And the diagram on the right shows a network that gets some inputs and produces some outputs. But there's problems with using a feed-forward neural network. We have to decide in advance what the maximum number of digits is both for both of the input numbers and for the output number. And more importantly, the processing that we apply to the different bits of the input numbers, doesn't generalize.
That is, when we learn how to add up the last two digits and deal with the carries, that knowledges in some weights. And as we go to a different part of a long binary number, the knowledge will have to be in different weights. So we won't get automatic generalization.
As a result, although you can train a neuron feedfoward neural network, and it will eventually learn to do binary addition on fixed-length numbers, it's not an elegant way to solve the problem. This is a picture of the algorithm for binary addition. The states shown here are like the states in a hidden Markov model, except they're not really hidden. The system is in one state at a time. When it enters a state it performs an action. So it either prints a one or prints a zero and when it's in a state it gets some input, which is the two numbers in the next column. And that input causes it to go into a new state. So if you look on the top right, It's in the carry station and it's just printed a one. If it sees a one, one, it goes back in to the same stage and print another one. If however it sees a one, zero or zero, one, It goes into the carry state but prints a zero. If it sees a zero, zero, it goes into the no carry state, and prints a one. And so on.
So a recurring neuro-net for binary edition needs to have two input units and one output unit. It's given two input digits at each time stamp. And it also has to produce an output at each time step. And the output is the output for the column that it took in two time steps ago. The reason we need a delay of two time steps, is that it takes one time step to update the hidden units based on the inputs, and another time step to produce the output from the hidden state. So the net looks like this. I only gave it three hidden units.
That's sufficient to do the job. It would learn faster with more hidden units, but it can do it with three. The three hidden units are fully interconnected and they have connections in both directions that don't necessarily have the same weight. In fact in general they don't have the same weight. The connections between hidden units allow the pattern of one time step to insensate the pattern of the next time step. The input units have feed forward connections to the hidden units and that's how it sees the two digits in a column.
And similarly, the hidden units have feed forward connections to the output unit and that's how it produces its output. It's interesting to look at what the recurring neural network learns. It learns four distinct patterns of activity in its three hidden units. And these patterns correspond to the nodes in the finite state automaton for binary addition.
We must confuse the units in a neural network, with the nodes in a final state automaton. The nodes in the finite state automaton correspond to the activity vectors of the recurrent neural network. The automaton is restricted to being exactly one state at each time. And similarly, the hidden units are restricted to have exactly one activity vector at each time in the recurrent neural network. So a recurrent neural network can emulate a finite state automaton but it's exponentially more powerful in its representation. With any hidden neurons, it has 2N to the N possible binary activity vectors.
Of course it only has n squared weights so it can't necessarily make full use of all that representational power. But if the bottleneck is in the representation a recurrent neural network can do much better than a finite state automaton. This is important when the input stream has two separate things going on at once. A finite state automaton needs to square its number of states in order to deal with the fact that there's two things going on at once. A recurrent neural network only needs to double its number of hidden units. By doubling the number of units, it does of course square the number of binary vector states that it has.
Why it is difficult to train an RNN
The backward pass is linear
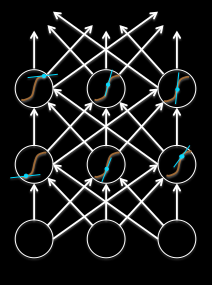
Figure 8: RNN backward pass
There is a big difference between the forward and backward passes. In the forward pass we use squashing functions (like the logistic) to prevent the activity vectors from exploding. The backward pass, is completely linear. If you double the error derivatives at the final layer, all the error derivatives will double.
- The forward pass determines the slope of the linear function used for back-propagating through each neuron.
The problem of exploding or vanishing gradients
What happens to the magnitude of the gradients as we back-propagate through many layers?
- If the weights are small, the gradients shrink exponentially.
- If the weights are big the gradients grow exponentially.
Typical feed-forward neural nets can cope with these exponential effects because they only have a few hidden layers.
In an RNN trained on long sequences (e.g. 100 time steps) the gradients can easily explode or vanish.
- We can avoid this by initializing the weights very carefully.
Even with good initial weights, its very hard to detect that the current target output depends on an input from many time-steps ago.
- So RNNs have difficulty dealing with long-range dependencies.
Why the back-propagated gradient blows up
If we start a trajectory within an attractor, small changes in where we start make no difference to where we end up. But if we start almost exactly on the boundary, tiny changes can make a huge difference.
Four effective ways to learn an RNN
Long Short Term Memory
Make the RNN out of little modules that are designed to remember values for a long time.
Hessian Free Optimization:
Deal with the vanishing gradients problem by using a fancy optimizer that can detect directions with a tiny gradient but even smaller curvature.
- The HF optimizer ( Martens & Sutskever, 2011) is good at this.
Echo State Networks:
Initialize the input → hidden and hidden → hidden and output → hidden connections very carefully so that the hidden state has a huge reservoir of weakly coupled oscillators which can be selectively driven by the input.
- ESNs only need to learn the hidden → output connections.
Good initialization with momentum
Initialize like in Echo State Networks, but then learn all of the connections using momentum.
Transcript
In this video, I'm going to talk about the exploding and vanishing gradients problem, which is what makes it difficult to train recurrent neural networks.
For many years, researchers in RNN networks thought they would never be able to train these networks to model dependencies over long time periods. But at the end of this video, I can describe four different ways in which that can now be done.
To understand why it's so difficult to train recurrent neural networks, we have to understand a very important difference between the forward and backward passes in a recurrent neural net. In the forward pass, we used squashing functions, like the logistic, to prevent the activity vectors from exploding. So, if you look at the picture on the right, each neuron is using a logistic unit shown by that blue curve and it can't output any value greater than one or less than zero, So that stops explosions.
The backward pass, however, is completely linear. Most people find this very surprising. If you double the error derivatives is it the final layers of this net, all the error derivatives will double when you back propagate. So, if you look at the red dots that I put on the blue curves, We'll suppose those are the activity levels of the neurons on the forward pass.
And so, when you back propagate, you're using the gradients of the blue curves at those red dots. So the red lines are meant to throw the tangents to the blue curves at the red dots. And, once you finish the forward pass, the slope of that tangent is fixed. You now back propagate and the back propagation is like going forwards though a linear system in which the slope of the non-linearity has been fixed.
Of course, each time you back propagate, the slopes will be different because they were determined by the forward pass. But during the back propagation, it's a linear system and so it suffers from a problem of linear systems, which is when you iterate, they tend to either explode or die. So when we backpropagate through many layers if the weights are small the gradients will shrink and become exponentially small.
And that means that when you backpropagate through time gradients that are many steps earlier than the targets arrive will be tiny. Similarly, if the weights are big, the gradients will explode. And that means when you back propagate through time, the gradients will get huge and wipe out all your knowledge. In a feed-forward neural net, unless it's very deep, these problems aren't nearly as bad because we typically only have a few hidden layers. But as soon as we have a recurrent neural network trained on a long sequence, for example 100 time steps, then if the gradients are growing as we back propagate, we'll get whatever that growth rate is to the power of 100 and if they're dying, we'll get whatever that decay is to the power of 100 and, so, they'll either explode or vanish.
We might be able to initialize the weights very carefully to avoid this and more recent work, shows that indeed careful initialization of the weights does make things work much better. But even with good initial weights, it's hard to detect the dependency of the current output or an input from many time-steps ago. So it's hard to make the output depend on things that happened a long time ago.
RNN's have difficulty dealing with long-range dependencies. Here's an example of exploding and dying gradients for a system that's trying to learn attractors. So suppose we try and train a recurrent neural network, So that whatever state we started in, it ends up in one of these two attractor states. So we're going a learn blue basin of attraction and a pink basin of attraction. And if we start anywhere within the blue basin of attraction, we will end up at the same point.
What that means is that, small differences in our initial state make no difference to where we end up. So the derivative of the final state with respect to changes in the initial state, is zero. That's vanishing gradients. When we back propagate through the dynamics of this system we will discover there's no gradients from where you start, and the same with the pink basin of attraction.
If however, we start very close to the boundary between the two attractors. Then, a tiny difference in where we start, that's the other side of the watershed, makes the huge difference to where we end up, that's the explosion gradient problem.
And so whenever your trying to use a recurrent neural network to learn attractors like this, you're bound to get vanishing or exploding gradients. It turns out, there's at least four effective ways to learn a recurrent neural network. The first is a method called long short term memory and I'll talk about that more in this lecture.
The idea is we actually change the architecture of the neural network to make it good at remembering things. The second method is to use a much better optimizer that can deal with very small gradients. I'll talk about that in the next lecture. The real problem in optimization is to detect small gradients that have an even smaller curvature. Heissan-free Optimization, tailored to your own apps is good at doing that.
The third method really kind of evades the problem. What we do is we carefully initialize the input to hidden weights and we very carefully initialize the hidden to hidden weights, and also feedback weights from the outputs to the hidden units. And the idea of this careful initialization is to make sure that the hidden state has a huge reservoir of weakly coupled oscillators. So if you hit it with an input sequence, it will reverberate for a long time and those reverberations are remembering what happened in the input sequence.
You then try and couple those reverberations to the output you want and so the only thing that learns in an Echo State Network is the connections between the hidden units and the outputs. And if the output units are linear, that's very easy to train. So this hasn't really learned the recurrent. It's used a fixed random recurrent bit, but a carefully chosen one and then just learned the hidden tripod connections.
And the final method is to use momentum, but to use momentum with the kind of initialization that was being used for Echo State Networks and that makes them work even better. So it was very clever to find out how to initialize these recurrent networks so they'll have interesting dynamics, but they work even better if you now modify that dynamic slightly in that direction that will help with the task at hand.
Neural Networks for Machine Learning Lecture 7e Long term short term memory Geoffrey Hinton Nitish Srivastava, Kevin Swersky Tijmen Tieleman Abdel-rahman MohamedLong Short Term Memory (LSTM) Hochreiter & Schmidhuber (1997) solved the problem of getting an RNN to remember things for a long time (like hundreds of time steps). They designed a memory cell using logistic and linear units with multiplicative interactions. Information gets into the cell whenever its “write” gate is on. The information stays in the cell so long as its “keep” gate is on. Information can be read from the cell by turning on its “read” gate. To preserve information for a long time in the activities of an RNN, we use a circuit that implements an analog memory cell.
- A linear unit that has a self-link with a
weight of 1 will maintain its state.
- Information is stored in the cell by
activating its write gate.
- Information is retrieved by activating
the read gate.
- We can backpropagate through this
circuit because logistics are have nice derivatives. keep gate 1.73 write gate input from rest of RNN read gate output to rest of RNNBackpropagation through a memory cell keep 0 keep 1 keep 1 1.7 1.7 read 0 write 1 1.7 keep 0 1.7 read 0 write 0 time à read 1 write 0 1.7Reading cursive handwriting This is a natural task for an RNN. The input is a sequence of (x,y,p) coordinates of the tip of the pen, where p indicates whether the pen is up or down. The output is a sequence of characters. Graves & Schmidhuber (2009) showed that RNNs with LSTM are currently the best systems for reading cursive writing.
- They used a sequence of
small images as input rather than pen coordinates.A demonstration of online handwriting recognition by an RNN with Long Short Term Memory (from Alex Graves) The movie that follows shows several different things: Row 1: This shows when the characters are recognized.
- It never revises its output so difficult decisions are more delayed.
Row 2: This shows the states of a subset of the memory cells.
- Notice how they get reset when it recognizes a character.
Row 3: This shows the writing. The net sees the x and y coordinates.
- Optical input actually works a bit better than pen coordinates.
Row 4: This shows the gradient backpropagated all the way to the x and y inputs from the currently most active character.
- This lets you see which bits of the data are influencing the decision.
Transcript
In this video, I'm going to talk about the back propagation through time algorithm. It's the standard way to train or recurrence your own network. The algorithm is really quite simple once you have seen the equivalents between a recurrent neural network and a feed forward neural network that has one layer for each time step. I'll also talk about ways of providing input, and desired outputs, to recurrent neural networks. So the diagram shows a simple recurrent net with three interconnected neurons. We're going to assume there's a time delay of one in using each of those connections and that the network runs in discrete time, so the clock that has integer ticks. The key to understanding how to train a recurrent network is to see that a recurrent network is really just the same as a feed forward network, where you've expanded the recurrent network in time. So the recurrent network starts off in some initial state. Shown at the bottom there, times zero. And then uses the way some of these connections to get a new state, shown at time one. You then uses the same weights again to get another new state, and it uses the same weights again to get another new state and so on. So it's really just a lead feed forward network, where the weight is a constraint to be the same at every layer. Now backprop is good at learning when there are weight constraints. We saw this for convolutional nets and just to remind you, we can actually incorporate any linear constraint quite easily in backprop. So we compute the gradients as usual, as if the weights were not constrained. And then we modify the gradients, so that we maintain the constraints. So if we want W1 to equal W2, we start off with an equal and then we need to make sure that the changing W1 is equal to the changing W2. And we do that by simply taking the derivative of the area with respect to W1, the derivative with respect to W2, and adding or averaging them, and then applying the same quantity for updating both W1 and W2. So if the weights started off satisfying the constraints they'll continue to satisfy the constraints. The backpropagation through time algorithm is just the name for what happens when you think of a recurrent net as a lead feet forward net with shared weights, and you train it with backpropagation. So, we can think of that algorithm in the time domain. The forward pass builds up a stack of activities at each time slice. And the backward pass peels activities off that stack and computes error derivatives each time step backwards. That's why it's called back propagation through time. After the backward pass we can add together the derivatives at all the different time step for each particular weight. And then change all the copies of that weight by the same amount which is proportional to the sum or average of all those derivatives. There is an irritating extra issue. If we don't specify the initial state of the all the units, for example, if some of them are hidden or output units, then we have to start them off in some particular state. We could just fix those initial states to have some default value like 0.5, but that might make the system work not quite as well as it would otherwise work if it had some more sensible initial value. So we can actually learn the initial states. We treat them like parameters rather than activities and we learn them the same way as learned the weights. We start off with an initial random guess for the initial states. That is the initial states of all the units that aren't input units And then at the end of each training sequence we back propagate through time all the way back to the initial states. And that gives us the gradient of the error function with respects to the initial state. We then just, adjust the initial states by following, that gradient. We go downhill in the gradient, and that gives us new initial states that are slightly different. There's many ways in which we can provide the input to a recurrent neural net. We could, for example, specify the initial state of all the units. That's the most natural thing to do when we think of a recurrent net, like a feed forward net with constrained weights. We could specify the initial state of just a subset of the units or we can specify the states at every time stamp of the subset of the units and that's probably the most natural way to input sequential data. Similarly, there's many way we can specify targets for a recurrent network. When we think of it as feed forward network with constrained weights, the natural thing to do is to specify the desired final states for all of the units. If we're trying to train it to settle to some attractor, we might want to specify the desired states not just for the final time steps but for several time steps. That will cause it to actually settle down there, rather than passing through some state and going off somewhere else. So by specifying several states of the end, we can force it to learn attractors and it's quite easy as we back propagate to add in derivatives that we get from each time stamp. So the back propegation starts at the top, with the derivatives for the final time stamp. And then as we go back through the line before the top we add in the derivatives for that man, and so on. So it's really very little extra effort to have derivatives at many different layers. Or we could specify the design activity of a subset of units which we might think of as output units. And that's a very natural way to train a recurrent neural network that is meant to be providing a continuous output.
blog comments powered by Disqus